7 8/9 As A Decimal
castore
Nov 24, 2025 · 9 min read
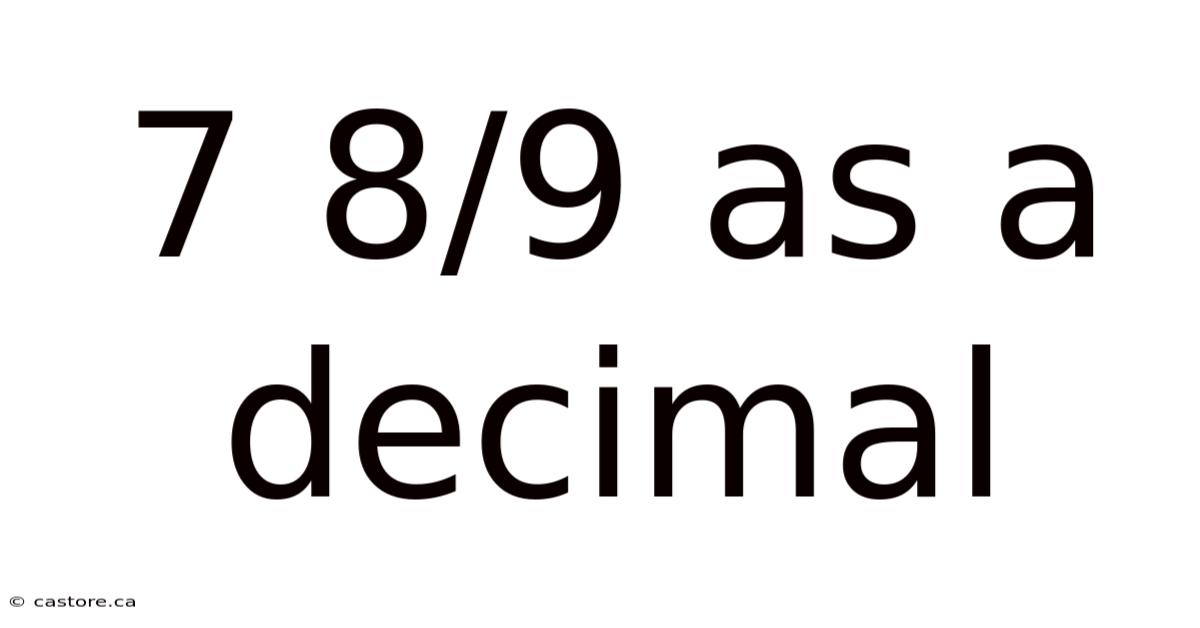
Table of Contents
Imagine you're baking a cake, and the recipe calls for 7 8/9 cups of flour. You grab your measuring cups, but they only have decimal markings. How do you measure out that precise amount? Or picture yourself working on a construction project, where accuracy is paramount. You need to cut a beam to exactly 7 8/9 inches. Again, you're faced with the challenge of converting this mixed number into a decimal for precise measurement.
Converting fractions, especially mixed numbers like 7 8/9, to decimals is a fundamental skill that bridges the gap between theoretical math and real-world applications. While fractions represent parts of a whole in a clear, relatable way, decimals provide a standardized format for calculations, measurements, and digital representations. Understanding how to perform this conversion not only enhances your mathematical literacy but also equips you with practical tools for everyday problem-solving. This article will explore the ins and outs of converting 7 8/9 into a decimal, providing a comprehensive guide to mastering this essential skill.
Unpacking the Mixed Number: 7 8/9
Before diving into the conversion process, let's break down what the mixed number 7 8/9 actually represents. A mixed number combines a whole number and a proper fraction. In this case, 7 8/9 signifies seven whole units plus an additional eight-ninths of another unit. This type of number is frequently used in everyday contexts because it’s easier to visualize and understand than an improper fraction (where the numerator is greater than or equal to the denominator).
Understanding the composition of mixed numbers helps contextualize the conversion to decimals. When we convert 7 8/9 to a decimal, we're essentially finding a single number that represents the same quantity in a different format. This conversion allows us to perform arithmetic operations, compare values, and use measurement tools that are designed for decimal inputs. The key lies in understanding how to handle the fractional part of the mixed number.
Comprehensive Overview: Converting Fractions to Decimals
The conversion of a fraction to a decimal is rooted in the fundamental relationship between these two mathematical forms. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). A decimal, on the other hand, represents a part of a whole using a base-10 system, where each digit after the decimal point represents a fraction with a denominator that is a power of 10 (e.g., tenths, hundredths, thousandths).
The underlying principle behind converting a fraction to a decimal is division. The fraction a/b is equivalent to a divided by b. This means that to convert any fraction to a decimal, you simply perform the division operation. The result will be a decimal representation of the fraction, which can be either a terminating decimal (ending after a finite number of digits) or a repeating decimal (having a pattern of digits that repeats infinitely).
For the mixed number 7 8/9, we must first focus on converting the fractional part, 8/9, to a decimal. The whole number part, 7, will remain as the whole number part of our final decimal. To convert 8/9 to a decimal, we divide 8 by 9. This division yields a repeating decimal: 0.8888... The repetition of the digit 8 continues infinitely.
When faced with repeating decimals, it's common practice to round the decimal to a certain number of decimal places, depending on the required precision. For example, rounding to two decimal places would give us 0.89, while rounding to three decimal places would give us 0.889. The more decimal places you include, the more accurate your representation will be.
Once we have the decimal representation of the fractional part, we simply add it to the whole number part of the mixed number. In this case, we add 7 to 0.8888... to get 7.8888... This is the decimal representation of the mixed number 7 8/9.
Trends and Latest Developments in Decimal Representation
In today's digital age, decimals are ubiquitous. They are used in computer programming, scientific calculations, financial transactions, and countless other applications. The ease with which decimals can be processed by computers and other digital devices has made them the preferred format for representing fractional values.
One significant trend is the increasing demand for higher precision in decimal representation. As technology advances and calculations become more complex, the need for more accurate decimal values has grown. This has led to the development of algorithms and software libraries that can handle decimals with a large number of digits.
Another trend is the use of different rounding methods. While the traditional method of rounding up or down based on the value of the next digit is still widely used, other methods, such as rounding to the nearest even number, are gaining popularity. These alternative methods can help to reduce bias in statistical calculations and other applications.
Furthermore, there's a growing awareness of the limitations of decimal representation. While decimals are convenient for many purposes, they cannot represent all rational numbers exactly. For example, the fraction 1/3 has a repeating decimal representation (0.3333...), which means that it can only be approximated using a finite number of digits. This limitation can be important in certain applications where exact values are required.
Tips and Expert Advice for Accurate Conversions
Converting fractions to decimals might seem straightforward, but accuracy is paramount, especially in practical applications. Here are some expert tips to ensure your conversions are precise:
-
Understand Repeating Decimals: As we've seen with 8/9, some fractions result in repeating decimals. Know how to identify these and use the correct notation (a bar over the repeating digits) or round appropriately based on the required level of precision. Ignoring the repeating nature can lead to significant errors in calculations. For example, if you were calculating the total length of several pieces of material, even a small error in each piece could accumulate and result in a substantial discrepancy.
-
Choose the Right Level of Precision: The level of precision required depends on the context. In some cases, rounding to two decimal places might be sufficient, while in others, you might need to go to several decimal places. Consider the impact of rounding errors on your final result. If you're working with financial data, for example, even a small rounding error can have significant consequences. Therefore, it’s important to understand the acceptable margin of error in your specific application.
-
Use a Calculator or Software for Complex Conversions: For complex fractions or when high precision is required, don't hesitate to use a calculator or software. These tools can handle the calculations quickly and accurately, reducing the risk of human error. Many online calculators are available that can convert fractions to decimals with a high degree of precision. Additionally, spreadsheet software like Microsoft Excel or Google Sheets can perform these conversions using built-in functions.
-
Double-Check Your Work: Always double-check your calculations, especially when dealing with critical measurements or financial data. A simple mistake can have significant consequences, so it's always better to be safe than sorry. One effective method is to use a different conversion tool or method to verify your result. For instance, if you initially used long division, you could use an online calculator to confirm your answer.
-
Convert Back to Fraction (if Possible): As a final check, especially when you've rounded the decimal, try to convert the decimal back into a fraction (or a simplified fraction) to see if it approximates the original fraction. This can help you identify any significant errors in your conversion or rounding. While the converted fraction might not be exactly the same due to rounding, it should be very close to the original fraction.
FAQ: Decoding Decimal Conversions
Q: How do I convert a mixed number to a decimal?
A: First, convert the fractional part of the mixed number to a decimal by dividing the numerator by the denominator. Then, add the resulting decimal to the whole number part of the mixed number. For 7 8/9, divide 8 by 9 to get approximately 0.8888... and add it to 7, resulting in 7.8888...
Q: What is a repeating decimal, and how do I handle it?
A: A repeating decimal is a decimal that has a pattern of digits that repeats infinitely. To handle repeating decimals, you can either use the correct notation (a bar over the repeating digits) or round the decimal to a certain number of decimal places, depending on the required precision.
Q: How do I determine the appropriate level of precision when rounding decimals?
A: The level of precision required depends on the context. Consider the impact of rounding errors on your final result. If you're working with financial data, for example, you might need to use more decimal places than if you're working with rough estimates.
Q: Can all fractions be converted to terminating decimals?
A: No, only fractions whose denominators have prime factors of 2 and/or 5 can be converted to terminating decimals. For example, 1/2, 1/4, and 1/5 can be converted to terminating decimals, while 1/3, 1/6, and 1/7 result in repeating decimals.
Q: Is it better to leave a fraction as a fraction or convert it to a decimal?
A: It depends on the situation. Fractions are often more accurate than decimals, especially when dealing with repeating decimals. However, decimals are often more convenient for calculations and comparisons. Choose the format that best suits your needs.
Conclusion
Converting fractions to decimals is a foundational skill with vast practical applications. Converting 7 8/9 to a decimal involves understanding the relationship between fractions and decimals, performing division, and handling repeating decimals with appropriate rounding. By understanding the principles and utilizing the tips provided, you can confidently tackle any conversion challenge, ensuring accuracy and precision in your work.
Now that you've mastered converting 7 8/9 to a decimal, put your skills to the test! Try converting other mixed numbers to decimals and see how you can apply this knowledge in your daily life, whether it's in the kitchen, the workshop, or the classroom. Share your experiences and insights in the comments below, and let's continue to explore the fascinating world of mathematics together!
Latest Posts
Latest Posts
-
Which Lobe Of The Brain Is Responsible For Smell
Nov 24, 2025
-
What Is Jaw Bone Cancer
Nov 24, 2025
-
Where Can I Buy Ephedrine
Nov 24, 2025
-
How To Massage Stomach For Digestion
Nov 24, 2025
-
7 8 9 As A Decimal
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about 7 8/9 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.